Statistik i biologien

Hvad er statistik, og hvorfor er det overhovedet relevant i biologien? Det korte svar kunne være, at det er en matematisk genvej til at spare tid og penge i forbindelse med f.eks. laboratorieforsøg. Men statistik kan også benyttes til at verificere resultater, således at man kan bevise en sammenhæng og konkludere, at resultaterne ikke bare er en tilfældighed. Kort sagt ville det meste videnskabelige arbejde (og meget andet arbejde) være stærkt hindret, hvis det ikke kunne bevise noget, eller hvis det ikke kunne foretage rationelle vurderinger om, hvor ens tid og penge skulle sættes ind for at opfinde ny viden. Det er her statistikken bliver en hjælp.

I denne korte artikel vil statistik blive præsenteret som fagdisciplin og relateret til biologien og forsøgsarbejdet i projektet Mennesket på en DNA-mikrochip. Specielt vil t-test blive gennemgået, som er af stor værdi for analysen af DNA-mikrochipeksperimenter. Statistik kan opdeles i flere forskellige kategorier, men er generelt en fagdisciplin under den anvendte matematik. I denne artikel benyttes to overordnede kategorier til inddelingen af den statistiske teori, nemlig den deskriptive statistik og statistisk inferens.

Den deskriptive statistik

Deskriptiv statistik dækker over den del af statistikken, der benyttes til at beskrive (engelsk: describe) data. Dette kan f.eks. være gennemsnit, største- og mindsteværdier og variation. I det følgende vil flere af de mest essentielle begreber blive defineret og beskrevet kort. Flere af disse begreber benyttes i statistisk inferens.

Gennemsnit

Det måske vigtigste nøgletal, der kan udregnes af en mængde data er gennemsnittet (også kaldt middelværdien). Dette tal kan f.eks. beskrive to fodboldspilleres præstationer og fortælle, at en spiller, der har scoret 10 mål i 13 kampe, scorer oftere end en spiller, der har scoret 30 mål i 500 kampe (selvom den sidstnævnte har scoret flest). Den konkrete matematiske formel for gennemsnittet er angivet herunder.

Ligning 1: Gennemsnit / middelværdi

$mu = frac{1}{n}cdot sum_{i=1}^{n} x_{i} = frac{x_{1}+x_{2}+...+x_{n}}{n} = sum_{i=1}^{n}x_{i} cdot f(x_{i})$

I ovenstående udtryk er der tre udgaver af samme formel, som kan benyttes til at beregne et gennemsnit. I korthed fortæller den første formel, at gennemsnittet, μ, beregnes ved at lægge alle data (x_i) sammen og dele med antallet af data (n). Summationstegnet angiver, at summen af alle værdier (fra værdi nr. 1 frem til n) skal lægges sammen. Dette skrives ved, at i går fra 1 (dvs. første dataværdi) til n (dvs. n’te dataværdi). Alternativt kan den første formel også skrives som den midterste. Summationstegnet er således en forkortet skrivemåde. Den tredje formel benytter sig imidlertid af frekvensen, f(x_i), for de forskellige dataværdier (dvs. hvor ofte en given dataværdi optræder). Frekvensen er defineret som:

$f(x_{i}) = frac{n_{i}}{n_{total}}$

Hvor n_i er antallet af gange en given værdi optræder ud af det totale antal værdier i et datasæt, n_total.

Median

En anden værdi, som minder om gennemsnittet, er medianen. Medianen angiver det midterste tal i en sorteret talrække. F.eks. er medianen af tallene 1, 4 og 7 lig med 4. Følgende korte eksempel viser, hvordan medianer findes:

Eksempel 1 – Median

Data: 2 4 6 7 8 9 11 Median = 7

Hvis der er et lige antal dataværdier, så er medianen gennemsnittet af de to midterste værdier, som eksemplificeret nedenfor:

Eksempel 2 – Median

Data: 2 4 6 7 8 9 Median = 6,5

Men hvad kan medianen fortælle, når man ligeså godt kan beregne gennemsnittet (median og gennemsnit ligger ofte tæt på hinanden)? Medianen er mere stabil over for ekstreme værdier, hvorfor medianen kan være en fordel at beregne i tilfælde med såkaldte ”outliers” (dataværdier som helt tydeligvis er usandsynlige i eksperimenter). Fordelen ved medianen kan illustreres ved følgende eksempel, hvor en ekspedient har noteret prisen for en liter mælk i ni dage:

Eksempel 3 – Median vs. Gennemsnit

Data: 5 6 5 6 7 8 6 5 99999 (enhed: kr.)

Gennemsnit, μ = 11116,33 kr.

Median = 6 kr.

I dette tilfælde, hvor ekspedienten tydeligvis har tastet forkert (eller læst en forkert pris) blev gennemsnittet stærkt påvirket (og størrelsen af gennemsnittet er ubrugelig), mens medianen ikke ville have ændret sig – uanset størrelsen af den niende værdi.

Varians

En anden vigtig faktor i den deskriptive statistik er variationen. Som det kan ses i eksempel 3 kan en stor variation i datasættet (den højeste værdi var 99999 kr. og laveste 5 kr.) føre til en ubrugelig værdi for gennemsnittet (ingen priser var i nærheden af 11116,33 kr.). Til at beskrive variationen i datasættet beregnes variansen af datasættet. Formlen for varians er angivet herunder:

Ligning 2: Varians

$sigma^{2} = frac{1}{n-1} cdot sum_{i=1}^{n}(x_{i}-mu)^{2} = frac{1}{n-1} cdot ((x_{1}-mu)^{2} +(x_{2}-mu)^{2} +...+ (x_{n}-mu)^{2} ) = sum_{i=1}^{n}(x_{i}-mu)^{2} cdot f(x_{i})$

Variansen σ² beregnes som beskrevet: Først findes forskellen på hver enkelt dataværdi (x_i) og gennemsnittet (μ), og denne forskel kvadreres. Derefter lægges alle disse (x_i– μ)²-værdier sammen, og denne sum divideres med (n – 1), som er antallet af dataværdier minus 1. Den sidste udgave af formlen for varians benytter sig af frekvensen for dataværdierne. Denne udgave kan ofte være mere brugbar, hvis der haves en stor datamængde, men såfremt antallet af dataværdier er mindre end 20 bør denne formel ikke benyttes, da den leder frem til et andet resultat. Dette skyldes, at denne formel benytter sig af frekvens (hvor der divideres med n, og ikke (n – 1) som egentligt er korrekt).

Variansen kan forstås som den gennemsnitlige kvadratiske afvigelse på alle dataværdierne. Årsagen til, at forskellene kvadreres, er, at negative afvigelser og positive afvigelse ikke må gå ud med hinanden. Effekten af dette kan ses i eksempel 4. Årsagen til at der divideres med (n – 1) og ikke n, er rent matematisk, at det ikke er antallet af værdier, men antallet af frihedsgrader, der skal divideres med. Dette gør næsten ingen forskel, når n er tilstrækkelig stor, men vil have større betydning for små n. Antallet af frihedsgrader vil ikke blive uddybet i denne artikel, men det bør noteres, at denne værdi (ofte kaldet v) benyttes i de fleste statistiske sammenhænge af årsager, som ligger uden for denne artikels formål at beskrive.

Eksempel 4 – Varians

Data: 2 3 5 6

Gennemsnit, μ = 4

Hvis ikke forskellene, (x_i– μ), havde været sat i anden potens, ville regnestykket have set således ud:

Dette ville fejlagtigt have givet det indtryk, at der ingen variation er i datasættet

Standardafvigelse

Standardafvigelsen, σ, er tæt beslægtet med variansen, idet standardafvigelsen netop er kvadratroden af variansen (variansen er standardafvigelsen i anden potens, σ²). Formlen for standardafvigelsen kan ses herunder:

Ligning 3: Standardafvigelse

$sigma = sqrt{ frac{1}{n-1} cdot sum_{i=1}^{n}(x_{i}-mu)^{2}} = sqrt{ frac{1}{n-1} cdot ((x_{1}-mu)^{2} + (x_{2}-mu)^{2} +...+ (x_{n}-mu)^{2}) } = sqrt{sum_{i=1}^{n}(x_{i}-mu)^{2} cdot f(x_{i})}$

Igen bemærkes det, at den sidste formel kun bør benyttes, såfremt man har mere end 20 dataværdier. Standardafvigelsen er ofte angivet i stedet for variansen af datasættet. Et eksempel på, hvordan standardafvigelsen beregnes kan ses i eksempel 5.

Eksempel 5 – Standardafvigelse

Data: 2 6 9 11

Gennemsnit, μ = 7

Statistiske plots

For at visualisere data findes der et hav af forskellige typer af plots og diagrammer. I denne artikel vil to af disse plots blive beskrevet – nemlig boksplottet (boks-plottet) og histogrammet.

Boksplot

Et boksplot afbilder data på en sådan måde, at området mellem 1. kvartil og 3. kvartil er et rektangel, 2. kvartil (medianen) en streg beliggende i dette rektangel, og fra rektanglet udgår en linje ud til både største- og mindsteværdien. To eksempler på et boksplot kan ses figur 23.

Boksplottets funktion er at skabe et hurtigt overblik over omfanget af et datasæt og angive beliggenheden af de forskellige kvartiler for at give en idé om, hvorvidt data primært er samlet omkring medianen, eller om data ligger spredt mere ud over hele skalaen. Undertiden hvis datamængden er meget stor vil de linier, der udgår fra rektanglet ikke gå ud til hhv. største- og mindsteværdi, men derimod til 5’te procentilen og 95’te procentilen.

Figur 23. Boksplots af to forskellige datasæt. Et boksplot afbilder data, således at både mindsteværdi, størsteværdi, median samt 1. og 3. kvartil kan aflæses.

Histogram

Et histogram er en anden og meget typisk måde af afbilde data på. I et histogram inddeles data i forskellige intervaller af tal såsom [1;3[, [3;5[ osv. (fra og med 1 til 3, hvor værdien 3 først er med i det næste interval, fra og med 3 til 5, osv.). Antallet af observationer inden for disse intervaller angives. Ved afbildning af intervaller vil det midterste tal i intervallet ofte være angivet på x-aksen i histogrammet og bredden af søjlerne svarer til intervallernes bredde. Antallet af observationer eller frekvensen i et givent interval vil kunne aflæses på y-aksen. Et eksempel på et histogram kan ses i figur 24, hvor intervallerne er [131;133[med midterværdien 132, [133;135[ med midterværdien 134 osv.

Figur 24. Et histogram afbilder antallet af observationer indenfor en given kategori.

Statistisk inferens

Indtil nu i artiklen har det handlet om deskriptiv statistik. Dvs. at statistikken har været brugt til at beskrive data, uden at denne beskrivelse har kunnet føre frem til konklusioner omkring udfald af nye forsøg. Statistisk inferens betegner metoder til at konkludere og fastsætte generelle tendenser og kvantitative egenskaber ud fra stikprøvetagning. Som beskrevet i indledningen til artiklen ligger betydningen af statistikken netop i at kunne forudsige- og fastsætte værdier og planlægge forsøg, f.eks. stikprøvetagning, på en økonomisk fordelagtig måde. Det ville f.eks. være uoverskueligt dyrt for en avis i en meningsmåling at udspørge alle danskere om deres politiske holdning. Derfor undlader alle aviser dette ved at tage repræsentative stikprøver i befolkningen. Herved kan de med en eller anden grad af konfidens (f.eks. med 95 % sikkerhed) lave en meningsmåling ud fra et par tusind danskere. Men hvordan tager man en repræsentativ stikprøve, altså en stikprøve, der repræsenterer befolkningen? Dette er altid en udfordring for de folk, der skal foretage en statistisk undersøgelse. En metode til at udtrække en tilfældig stikprøve i befolkningen kunne være at give alle danskere et nummer fra 1 til 5,4 mio. (befolkningstallet) og så udtrække helt tilfældige numre i denne række. Hvis man ville undersøge kornet fra en mark kunne man flyve højt op over marken og kaste nogle hulahopringe tilfældigt ud og så undersøge (tage målinger af) det korn, som var inden for de forskellige ringe. En dårlig måde at foretage en tilfældig stikprøveudvælgelse kunne f.eks. være at spørge alle gymnasieelever om deres politiske holdning og ud fra denne stikprøve udtale sig om hele befolkningen. Dette ville højst sandsynligt give et skævt billede, da alle gymnasieelever er i ca. samme aldersgruppe og alle har prioriteret deres uddannelse frem for arbejde.

En anden fejlagtig metode, som blev brugt i USA i starten af 1900-tallet var at ringe rundt og spørge, hvem folk stemte på til næste præsidentvalg. Da det kun var de rigeste, der havde råd til en telefon, gav dette også et helt forkert indtryk af den politiske situation. Den kandidat, som ifølge meningsmålinger klart ville vinde, tabte stort ved selve valget. Nu om dage ville en telefonrundspørge dog næppe være helt så fejlbehæftet.

Når man har taget en repræsentativ stikprøve, skal det ud fra statistiske tests vurderes, hvor overbevisende resultatet fra forsøget er. En typisk metode at gøre dette på er hypotesetests. Her defineres to hypoteser, som oftest kaldes nulhypotesen, H₀, og den alternative hypotese, H₁. Oftest vil den alternative hypotese være det, man ønsker at vise. Og for at vise denne må man forkaste nulhypotesen (vise at denne ikke kan gælde). F.eks. kunne nulhypotesen være, at et gennemsnit er lig med 3, og den alternative hypotese, at gennemsnittet ikke er 3. Hvis man således kan forkaste/afvise nulhypotesen, har man vist, at den alternative hypotese med stor sandsynlighed gælder.

t-test for ét gennemsnit

En klassisk metode til at foretage en hypotesetest er den såkaldte t-test. Denne metode benyttes typisk til test af et gennemsnit ved en stikprøvetagning. t-testen gælder kun, når det kan antages, at det datamateriale, der skal undersøges, er normalfordelt. Normalfordelingen gælder f.eks. for vægten af mandlige studerende, den præcise vægt af 100 gram slikposer og højden af 25-årige kvinder. Men den gælder ikke, hvis data fra forskellige stærkt inhomogene grupper er blandet sammen, f.eks. vægten af blåhvaler og mandlige studerende. Her vil data på ingen måde være normalfordelte. Det er desuden vigtigt at bemærke, at det ikke nødvendigvis er den stikprøve, man har taget, som i sig selv skal være normalfordelt. Derimod er det den samlede mængde data, som stikprøven tages fra, som skal være normalfordelt. Dette vil f.eks. sige, at en stikprøve bestående er fire højder af tilfældige mandlige studerende ikke behøver at være normalfordelt i sig selv, men derimod, at samtlige højder af alle mandlige studerende (i hele Danmark) skal være normalfordelt, for at man kan foretage en t-test på datamaterialet (f.eks. de fire højder). Normalfordelinger vil ikke blive beskrevet nærmere i denne artikel, men på figur 25 kan typiske normalfordelingskurver ses. Det fremgår, at disse er symmetriske med toppunkt i gennemsnitsværdien, μ. Desuden bør det bemærkes, at variansen eller standardafvigelsen ofte er angivet på sådanne kurver, eftersom 95,4 % af data i en normalfordelingskurve ligger i intervallet μ ± 2σ, også skrevet [μ – 2σ; μ + 2σ].

Figur 25. Forskellige normalfordelingskurver.

Hvis det kan antages, at data er normalfordelte, skal nulhypotesen og den alternative hypotese defineres, inden der foretages beregninger. Typisk vil dette kunne skrives således:

Nulhypotese: μ = μ₀

Alternativ hypotese: μ ≠ μ₀

Eller: μ < μ₀

Eller: μ > μ₀

De to ”eller” betyder, at man enten kan undersøge, om det faktiske gennemsnit er forskelligt fra, mindre end eller større end det gennemsnit, som nulhypotesen er defineret til. Herefter foretages beregningerne. Formlen, der benyttes til en t-test, er angivet herunder:

Ligning 4: t-test for ét gennemsnit

$t = frac{bar{x}-mu_{0}}{s/sqrt{n}}$

Antal frihedgrader: v = n – 1

I denne formel betegner n størrelsen af stikprøven, X betegner gennemsnittet på stikprøven (i modsætning til μ, der betegner det ”sande” gennemsnit for samtlige dataværdier, som ikke nødvendigvis er med i ens stikprøve), μ₀ betegner det gennemsnit, der er defineret i nulhypotesen, S betegner standardafvigelsen for stikprøven (i modsætning til σ, som er standardafvigelsen for alle dataværdier, som ikke nødvendigvis er med i stikprøven), og t er den parameter, der beregnes. Antallet af frihedsgrader, v, benyttes i forbindelse med opslag i t-tabel og vil blive beskrevet senere.

En sidste parameter, der skal defineres, er α. Denne parameter angiver graden af usikkerhed for den endelige konklusion (f.eks. hvis α = 0,05, kan man konkludere noget med 95 % sikkerhed eller 5 % usikkerhed). Når denne parameter er defineret (α skal ligge mellem 0 og 1, også skrevet mellem 0 og 100 %), foretages beregningerne, og ud fra følgende skema foretages konklusionen:

Alternativ hypotese H₁	Forkast hvis H₀
μ < μ₀	t < –t_α
μ > μ₀	t > t_α
μ ≠ μ₀	t < –t_α/2 Eller t > t_α/2

t_α-værdierne benyttes til at afgøre t-testens udfald, og disse findes ved opslag i en t-tabel. Oftest vil der i tabellerne kun være t_α-værdier for udvalgte α og for udvalgte v (antal frihedsgrader). Derfor er man tit nødt til at finde den tætteste, brugbare værdi. I eksempel 7 udføres en t-test på en stikprøve.

t-test for to gennemsnit

Nogle gange er det nok kun at foretage en t-test for ét gennemsnit, men ofte er meningen med beregningen at påvise en forskel på to grupper (populationer). F.eks. i biologien kan det i forbindelse med DNA-mikroarrays være relevant at kunne påvise, at der rent faktisk er en forskel på en gruppe celler og en anden (f.eks. en gruppe raske celler og en gruppe kræftceller) ved målinger på en given celleparameter (f.eks. udtrykkelsen af et protein). Til dette formål kan en t-test for to gennemsnit benyttes. Ligesom før skal data (for begge grupper) være normalfordelte, og der skal defineres en nulhypotese og en alternativ hypotese. Typisk ønskes det vist, at to gennemsnit er forskellige. Nulhypotesen vil derfor være, at de to gennemsnit er ens, og den alternative hypotese at de er forskellige:

Nulhypotese: μ₁– μ₂ = 0

Alternativ hypotese: μ₁ – μ₂ ≠ 0

Eller: μ₁ – μ₂ < 0

Eller: μ₁ – μ₂ > 0

Igen er der flere muligheder for den alternative hypotese. Konklusionen foretages på baggrund af et lignende skema som før, efter at en α-værdi er blevet valgt.

Alternativ hypotese H₁	Forkast hvis H₀
μ₁ – μ₂ < 0	t < –t_α
μ₁ – μ₂ > 0	t > t_α
μ₁ – μ₂ ≠ 0	t < –t_α/2 Eller t > t_α/2

t_α-værdierne benyttes igen til at afgøre t-testens udfald. Disse t_α-værdier findes igen ved opslag i en t-tabel. Formlen, der benyttes til en t-test for to gennemsnit, er angivet herunder:

Ligning 5: t-test for to gennemsnit

$t=frac{bar{x_{1}}-bar{x_{2}} }{S_{p}/sqrt{ frac{1}{n_{1}}+frac{1}{n_{2}} } }$

Antal frihedgrader: v = n₁ + n₂ – 2

$S_{p} = sqrt{ frac{(n_{1}-1) cdot S_{1}^{2} + (n_{2}-1) cdot S_{2}^{2}) }{ n_{1}+n_{2}-2 } }$

I denne formel betegner n₁ og n₂ størrelsen af stikprøven fra hhv. population 1 og population 2, X₁ og X₂ betegner gennemsnittet på stikprøven fra hhv. population 1 og population 2. S_p betegner den poolede standardafvigelse (den ”fælles” standardafvigelse, som er en slags gennemsnitlig standardafvigelse for stikprøverne). Den beregnes efter ovenstående formel ud fra S₁ og S₂, som er standardafvigelsen for stikprøven for hhv. population 1 og population 2. Igen er t den parameter, der bestemmes. Bemærk, at antallet af frihedsgrader nu beregnes efter en ny formel. Et eksempel på hvordan en t-test for to gennemsnit benyttes, er givet i eksempel 8.

Konfidensinterval

Et sidste statistisk begreb, der vil blive præsenteret i denne artikel, er konfidens-intervallet. Konfidensintervallet benyttes til at udtrykke, at et gennemsnit for nogle data med en given sikkerhed ligger inden for et interval (f.eks. at gennemsnittet for antallet af æbler på et æbletræ med 90 % sandsynlighed ligger mellem 100 og 200). Til at lave et konfidensinterval benyttes mange af de samme parametre som ved t-test, og ofte laves der et konfidensinterval efter en t-test er udført. Formlen for konstruktionen af et konfidensinterval er givet ved:

Ligning 6: konfidensinterval for middelværdien

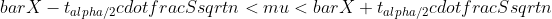
$bar{X} - t_{alpha/2} cdot frac{S}{sqrt{n}} < mu < bar{X}+t_{alpha/2}cdot frac{S}{sqrt{n}}$

Antal frihedsgrader: v = n – 1

Her betegner n størrelsen af stikprøven, X betegner gennemsnittet på stikprøven, μ betegner hele populationens gennemsnit, S betegner standardafvigelsen for stikprøven, og t_α/2 er en t-parameter, der slås op i en t-tabel ud fra valg af α og antallet af frihedsgrader. Et eksempel på, hvordan et konfidensinterval beregnes, er givet i eksempel 9.

En vigtig pointe ved konfidensintervaller er, at når et sådant interval er beregnet, kan man udelukke alle værdier, som ikke indgår i intervallet med den givne procents sikkerhed. Dvs. hvis man startede med at udregne konfidensintervallet fra eksempel 9, kunne man hurtigt konkludere, at gennemsnittet for hele populationen med 95 % sikkerhed ikke er 10 (som det blev vist i eksempel 7). Det kan derfor være en stor fordel at udregne et konfidensinterval for et gennemsnit, når man har taget en stikprøve. Man kan så, uden at skulle lave mange t-tests, hurtigt afvise alle værdier, der ikke ligger inden for intervallet.

For sammenligning af to gennemsnit kan et konfidensinterval også benyttes. I dette tilfælde er konfidensintervallet givet ved følgende formel:

Ligning 7: Konfidensinterval for forskellen på to gennemsnit

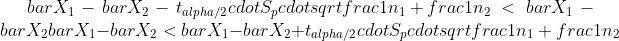
$bar{X_{1}} - bar{X_{2}} - t_{alpha/2} cdot S_{p} cdot sqrt{frac{1}{n_1} + frac{1}{n_{2}}} < bar{X_{1}} - bar{X_{2}} bar{X_{1}} - bar{X_{2}} < bar{X_{1}} - bar{X_{2}} + t_{alpha/2} cdot S_{p} cdot sqrt{frac{1}{n_1} + frac{1}{n_{2}}}$

Hvor

$S_{p} = sqrt{frac{(n_{1}-1)cdot S_{1}^{2} + (n_{2}-1)cdot S_{2}^{2} }{n_{1}+n_{2}-2}}$

Antal frihedsgrader: v = n₁ + n₂ – 2

I denne formel betegner n₁ og n₂ størrelsen af stikprøven fra hhv. population 1 og population 2, X₁ og X₂ betegner gennemsnittet på stikprøven fra hhv. population 1 og population 2. S_p betegner den poolede standardafvigelse. Den beregnes efter ovenstående formel ud fra S₁ og S₂, som er standardafvigelsen for stikprøven for hhv. population 1 og population 2. Størrelsen t_α/2 er en t-parameter, der slås op i en t-tabel ud fra valg af α og antallet af frihedsgrader. I eksempel 10 kan det ses, hvordan et konfidensinterval for forskellen på to gennemsnit kunne have været benyttet til nå til samme konklusion som i eksempel 8.

Relation til biologien

Statistik benyttes som redskab i mange fag. I biologien benyttes statistik specielt i forbindelse med udvikling af lægemidler, fastsættelse af biologiske parametre ud fra eksperimenter og sandsynliggørelse af biokemiske teorier. Bl.a. er statistik en fuldstændig nødvendighed for gennemførelsen af målinger med DNA-mikroarrays, hvor der typisk køres forsøg med forskellige typer celler. Da det er umuligt at teste alle kræftceller i en bestemt kræftsygdom i et DNA-mikroarray, endsige bare i en enkelt tumor, er det nødvendigt at kunne gennemføre pålidelige forsøg, som kan generalisere udfaldet af få eksperimenter til teorier og hypoteser omkring kræftudvikling og kræftbekæmpelse. Hertil bidrager statistikken, ved at den med en vis procents sikkerhed kan estimere værdien af en parameter (ofte inden for et konfidensinterval) ud fra stikprøver af hele cellepopulationer. I forbindelse med biologiske forsøg accepteres det generelt, at konklusionerne på forsøgene kun er 95 % sikre (f.eks. i en t-test med α-værdi på 5 %, eller et konfidensinterval på 95 %), men undertiden i strenge medicinske forsøg kan kravene til sikkerhed være endnu højere (ofte 99 % sikkerhed). Det er naturligvis altid sværere at påvise en sammenhæng eller estimere en værdi, hvis kravene til sikkerheden i resultatet forøges. Derfor er det normalt at kræve, at ens resultat er mellem 95 % og 99 % sikkert. Dette krav giver et relativt pålideligt resultat, samtidig med at denne afvigelse fra 100 % sikkerhed giver en enorm tidsbesparelse. En mindre stikprøve på nogle tusind kræftceller vil ofte være nok (såfremt stikprøven er repræsentativ!) til f.eks. at vurdere med 95 % sikkerhed, om kræftcellerne har en højere produktion af et givent protein ift. raske celler. Dette må mildt sagt siges at være lettere end at teste samtlige celler i en menneskekrop.

Til sidst bør det siges, at statistikken også har sine faldgruber. Ofte vil man gerne vise sammen-hænge (statistisk kaldt: at korrelere forsøgsresultater), men det kan undertiden være muligt at se statistiske sammenhænge mellem fænomener, som ikke er beslægtede. Det er f.eks. sandsynligt, at der ville kunne ses en sammenhæng mellem hudkræft og havbadning. Dette skyldes selvfølgelig ikke, at det at bade i havet er kræftfremkaldende. Derimod kunne det skyldes, at de personer, som bader i havet, sandsynligvis også er personer, som befinder sig meget i solen, og som derfor modtager en stråling, der kan være årsag til kræftudvikling. Det er derfor altid vigtigt nøje at overveje de sammenhænge og resultater, man vil prøve at vise, og være kritisk i ens analyse.